Mathematical Image Reconstruction

This MATLAB project completed in my Advanved Engineering Mathematics course demonstrates how eigenvectors and eigenvalues can be used for image re-synthesis and compression. I learned the following important takeaways by completing this project:
- Any image can be represented as a set of eigenpairs (eigenvalues and corresponding eigenvectors).
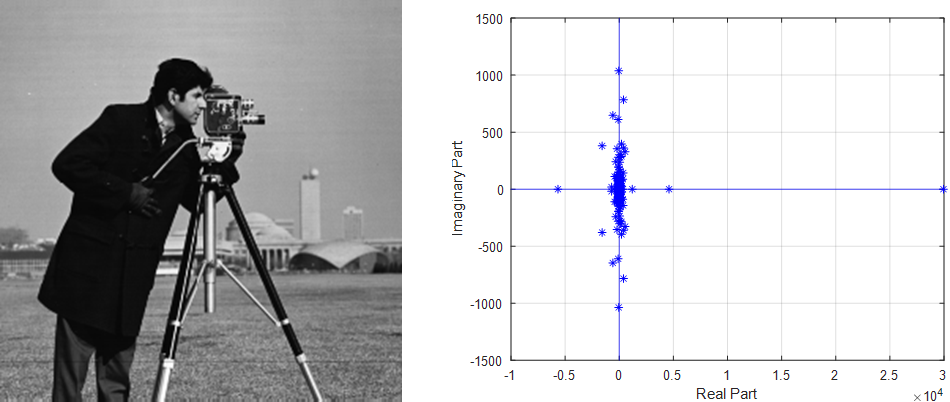
Original Cameraman Image and Plot of Eigenvalues
- Some image eigenvalues have greater magnitudes than others.
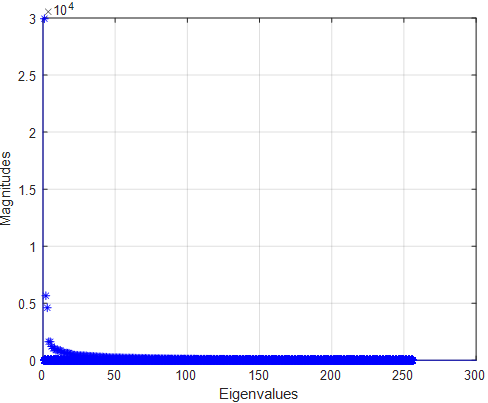
Magnitude of Eigenvalues of Image
- When reconstructing an image, eigenvalues with greater magnitudes contribute more information to the image than eigenvalues with smaller magnitudes when paired with their corresponding eigenvectors.

Re-Synthesized Image Using First 1, 5, 50, 100 Eigenvalues
- By finding the absolute error in pixel values between a reconstructed image and the original one, you can make an informed decision when dealing with a trade off between information storage and image quality. “Throwing away” the eigenpairs that contribute little to no important visual information can be used as a crude image compression algorithm.
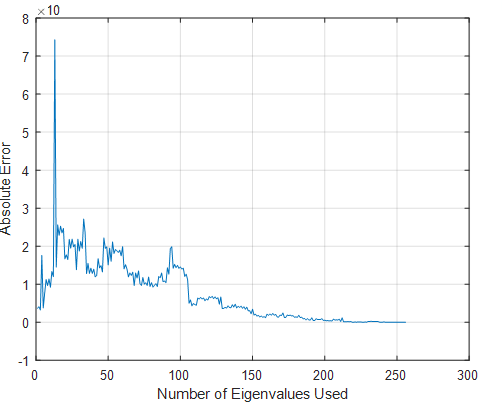
Re-Synthesis Absolute Error vs. Number of Eigenvalues Used

Re-Synthesized Image Using First 200 vs All Eigenvalues
More information about this project is available on GitHub.
