Mathematical Edge Detection

This MATLAB project completed in my Advanved Engineering Mathematics course demonstrates gradient and Laplacian edge detection techniques, and their caveats with grayscale images. I learned the following important takeaways by completing this project:
- Taking the gradient of an image in any direction (by convolving the image with a kernel) will result in an intuitive visualization of how quickly pixel values change in said direction. This can be used as a crude edge detection method.

Horizontal, Vertical, Magnitude Gradients of Cameraman Image
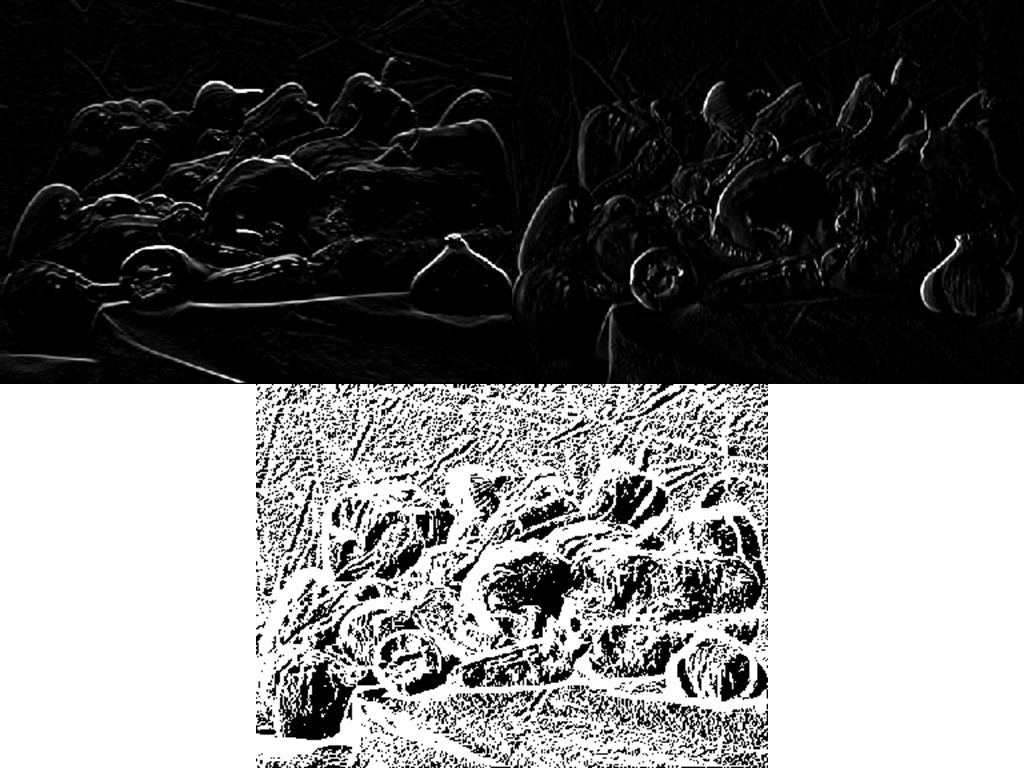
Horizontal, Vertical, Magnitude Gradients of Peppers Image
- Taking the Laplacian of an image (again, by convolving the image with a kernel) will result in a visualzation of the rate at which the gradients change in any direction. This serves as a much cleaner and comprehensive edge detection method than trying to take gradients in individual directions.

Laplacians of Cameraman and Peppers Images
- The mapping of an RGB image to grayscale is a huge loss in information, and it opens your edge detection algorithm to vulnerabilities. Since many RGB color combinations will get mapped to the same grayscale value, an edge that could be detected in the original three-dimensional space may not be detected in the new one-dimensional space.

Chosen RGB1, Chosen RGB2, Pure Blue and Grayscale Equivalent of Image

Gradient and Laplacian of Image
More information about this project is available on GitHub.
