Dancing Hexapod

The inspiration for my final project in my Principles of Robotics class stemmed from Boston Dynamics’ video of their dancing robots. I proposed the creation of a hexapod (six-legged) mobile robot that could accurately detect the tempo of a song or audio file being played, and perform a set of dance moves that are synchronized to the beat. As a stretch goal, I wanted the hexapod to move toward the audio source before dancing, just as a human would at a concert. The following initial flowchart depicts the desired behavior of the robot:
Program Flowchart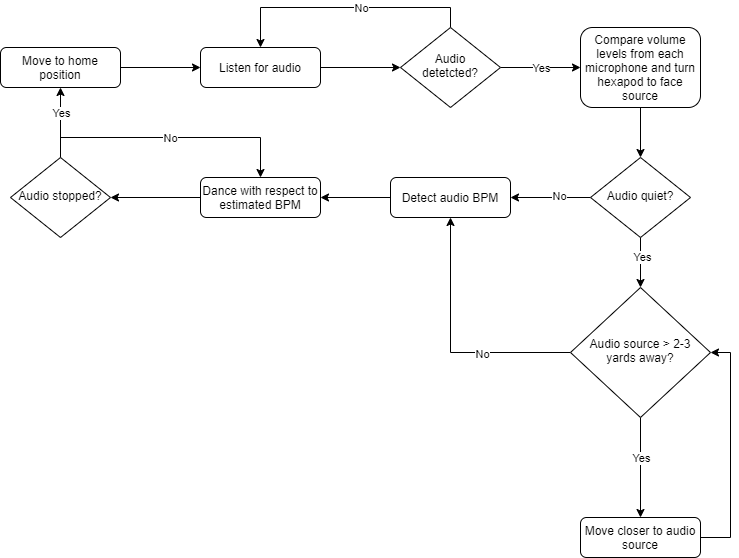
Control Boards
Hexapod Overhead View
The audio processing algorithm aimed to estimate the tempo of the audio in real time, but memory limitations on the Arduino UNO did not allow for this. Instead, I implemented the following algorithm:
- Capture and store audio samples from a microphone periodically
- Apply a Hamming window to the audio signal to improve clarity in the frequency domain
- Apply the Fast Fourier Transform to the windowed audio signal. The result is the frequency spectrum of the sample.
- Determine the highest peak of the frequency spectrum. This is the most prevalent frequency in the signal.
- Transform the peak frequency (f) to a reasonable one, if needed.*
- Set the delay between robot frame transformations accordingly. (Delay T = 1/f)
* Sometimes, the most prevalent frequency detected is actually a harmonic of the true tempo of the audio signal. To achieve an accurate estimate of the true tempo, it may be necessary to multiply or divide the detected peak frequency by an even integer. To simplify the determination of whether this is necessary, I only tested the algorithm on audio signals with tempos in the 1-3 Hz (60-180 BPM) range; most musical pieces fall within this range. Any detected peak frequency outside of this range was multiplied or divided by 2 until a value within the proper range was reached.
More information about this project is available on GitHub.
